4장 신경망 기초
퍼셉트론: 단순 모델로써 기계학습의 용어와 원리를 설명하는데 적합하다.
구조: 입력층과 출력층으로 구성 -> 입력층은 d+1개로 구성, 출력 층은 하나의 노드로 구성
Q.퍼셉트론의 연산과정에 대해 서술하시오.
- 입력층의 i번째 노드는 Xi와 Wi를 곱하여 출력노드로 전달한다.
- 이때 0번째 노드인 X0은 항상 1이다 (바이어스 노드)
- 출력 노드는 d+1 개의 곱셈 결과를 모두 더하여 s를 계산하고, 활성 함수를 적용한다.
+Q-1 퍼셉트론의 연산과정에 대해 서술하고, 이때 사용하는 활성 함수란 무엇인지 서술하시오.
+ 활성함수란 두뇌가 뉴런을 활성화하는 과정을 모방한 것인데, 퍼셉트론은 활성 함수를 계단 함수를 이용하여 s의 값이 0보다 크면 1을 출력하고 그렇지 않은 경우에는 -1을 출력한다. 따라서 퍼셉트론은 특징 벡터를 1과 -1로 분류하는 장치로써 이진 분류기라고 칭할 수 있다.(이진 분류의 예시: 생산라인에서 나오는 제품의 불량 유무, 환자와 정상인 등) 퍼셉트론은 특징 공간을 두 부분 공간으로 분할 하는 이진 분류기, 선형으로 국한 → 데이터셋이 어떠 한식으로 분포하든 선 하나로 분류 할 수 있는 데이터 셋이기만 한다면 퍼셉트론은 연결강도 값을 조절하여 어떠한 데이터 셋도 잘 분류해낼 수 있다.
퍼셉트론 학습 알고리즘
퍼셉트론을 학습하려면 손실 함수 J를 설계해야 하며, 손실 함수의 값을 낮추는 방법을 고안해야한다.
신경망의 학습 알고리즘 구현에 필요한 사항
- w(가중치)를 어떤 값으로 초기 설정해야하는지
- 손실 함수를 어떻게 정의할 것인가 → 오류의 양으로 측정
- 손실 함수 값을 낮추는 델타 w(가중치)를 어떻게 구할 것인가 → 미분을 사용
손실함수 J가 만족해야 할 조건:
- W가 훈련집합에 있는 샘플을 모두 맞히면, 즉 정확률이 100%면 J(w)는 0이다
- W가 틀리는 샘플이 많을 수록 J(w)의 값이 크다( 틀린 샘플이 많을 수록 손실 함수 값이 커진다)
X가 +1부류라면 퍼셉트론의 출력 wx^T는 음수이므로 -y(wk^T)은 양수
X가 -1부류라면 퍼셉트론의 출력 wx^T는 양수이므로 -y(wx^T)는 양수
경사하강법이란 미분을 이용하여 최적해를 찾는 기법
개념적: 전방계산->오차계산->후방가중치 갱신 반복
3가지 문제
분류: 지정된 몇가지 부류로 구분하는 문제
물체 검출: 바운딩 박스로 물체 위치를 찾아내는 문제
물체 분할: 화소 수준으로 물체를 찾아내는 문제
각 문제에 대한 적절한 손실함수 필요
분류: 참 값과 예측 값 차이를 손실 함수에 반영
물체 검출: 참 바운딩 박스와 예측한 바운딩 박스의 겹침 점도를 손실 함수에 반영트
물체 분할: 화소별로 레이블이 지정한 물체에 해당하는지 따지는 손실 함수
스토캐스틱 경사 하강법 배치모드 vs 패턴모드
알고리즘 4-4 기준으로
배치 모드: 틀린 샘플을 모은 다음 한꺼번에 매개 변수 갱신 (틀린 부분을 I집합에 모으는 방법)
패턴 모드: 패턴 별로 매개 변수 갱신 (틀린 부분에 대하여 곧바로 가중치 w를 갱신)
하지만 딥러닝에서는 미니 배치 사용: 패턴 모드와 배치 모드 사이
- 훈련 집합을 일정한 크기의 부분 집합으로 나눈다
- 부분 잡합으로 나눌 때 랜덤 샘플링을 적용하기 때문에 스토캐스틱 경사 하강법 이라고 부른다.
기계학습의 디자인 패턴 (sklearn의 디자인 패턴)
데이터 읽기 -> 모델 객체 생성 -> 모델 학습 -> 예측 -> 성능 평가
다층 퍼셉트론: 일반 퍼셉트론은 선형이라는 한계가 존재
그렇게 은닉층을 추가하여 비선형으로 확장한 개념이 다층 퍼셉트론
→ 복잡한 형태의 데이터셋이 주어질 경우에 기존의 퍼셉트론으로는 선형 분리 불가 →
하지만 선을 여러개 더할 경우에 분리 가능→ 예시로 4개의 선으로 분리하면 4개의 퍼셉트론을 사용했다 → 이 N개의 퍼셉트론을 출력을 입력으로 받는 또 다른 하나의 퍼셉트론을 연결하면 데이터셋을 비선형으로 분리할 수 있는 다층 신경망이 된다.
이때 다층신경망은 하나의 입력층과 한개이상의 은닉층과 출력층으로 이루어져 있다


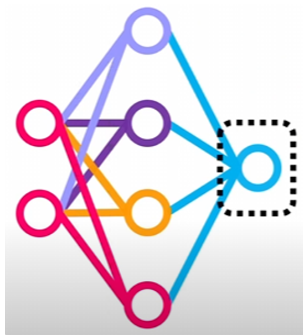

은닉 노드가 많으면 신경망 용량이 커지지만 과잉 적합 가능성이 높아진다
다층 퍼셉트론은 행렬계산이다
퍼셉트론이 활성 함수로 계단 함수를 사용했다면 다층 퍼셉트론은 시그모이드 함수를 활성 함수로 사용
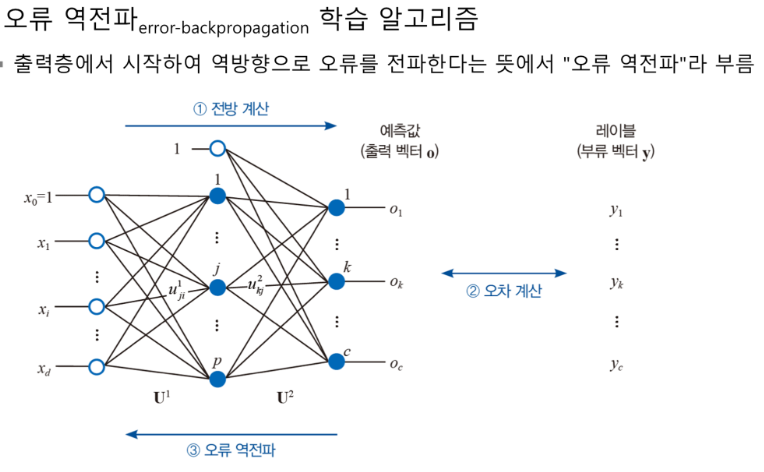
오류 역전파 학습 알고리즘: 출력층에서 시작하여 역방향으로 오류를 전파 하는 알고리즘
----------------------------------------------------------------------------------------------------------------
4장에서 나올 법한 예상 문제
4장
1. 퍼셉트론이란 무엇인가, 어떤 구조인지, 연산과정에 대해 설명
단순 모델로써 기계학습의 용어와 원리를 설명하는데 적합한 모델, 입력층과 출력층으로 구성되어 있으며 입력층은 d+1개, 출력층은 1개로 이루어져 있고 0번째 노드는 1인 바어어스 노드를 가지고 있다.
입력층의 각 노드들과 그 노드들에 연결된 가중치를 곱하여 모두 더해주고, 바이어스 노드의 가중치 값을 빼주어 나온 결과 값(s)을 활성함수인 계단 함수에 적용시켜 0<s 라면 1을 출력 0>s 라면 -1을 출력한다
2 . 신경망 학습 알고리즘을 구현하는데 필요한 사항은?
- w를 어떻게 초기 설정해야하는지
- 손실함수를 어떻게 정의할 것인가 (오류의 양으로 측정)
- 손실 함수를 낮추는 값 w를 어떻게 구할 것인지(미분)
3. 손실함수 J가 만족해야 하는 조건
- w가 훈련집합에 있는 모든 샘플을 맞추면, 즉 정확률이 100이면 J는 0이다
- w가 틀리는 샘플이 많을수록 J의 값은 크다(틀린 샘플이 많을 수록 손실 함수 J의 값이 커진다)
4. 경사하강법이란 무엇인지 서술하고 원리를 설명하시오
경사하강법은 미분을 이용하여 최적해를 찾는 기법이고,
임의의 시작점을 기준으로 현재 위치의 기울기를 구하고 그의 반대 방향으로 조금씩 이동하여 손실함수 값을 찾는다. 이렇게 측정 값을 기준으로 반대로 왔다 갔다 하며 손실 함수 값을 최저로 찾는 방법을 경사하강법이라고 한다
5. 퍼셉트론의 학습 알고리즘을 개념적으로 표현하시오
퍼셉트론은 입력층부터 전방 계산을 실시하고, 예측값을 출력해 기대값인 레이블과 오차를 비교하고 계산하여 후방으로 가중치를 갱신하는 학습 알고리즘이다.
6. 현대 기계학습 복잡도에서 발생할 수 있는 문제점 3가지
분류: 지정한 몇가지 부류로 분류하는 것
물체 검출: 바운딩 박스를 통하여 물체의 위치를 찾는 것
물체 분할: 화소 단위의 수준으로 물체를 찾아내는 문제
3가지 모두 적절한 손실 함수 값을 통해 해결
분류: 참값고 레이블 값의 차이를 손실 함수에 반영
검출: 참바운딩 박스와 레이블 바운딩 박스의 겹침 정도를 반영
분할: 화소별로 레이블이 지정한 물체에 해당하는지 따지는 손실 함수
7. 기계 학습에서 사용하는 스토캐스틱 경사하강법의 종류 3가지에 대해 설명하시오
배치모드 : 틀린 샘플을 모아 한꺼번에 매개 변수 갱신 (틀린 부분을 I집합으로 모으는 방법)
패턴모드: 패턴별로 매개 변수 갱신 (틀린 부분에 대하여 곧바로 가중치를 갱신)
미니배치 모드: 배치와 패턴모드의 사이
→ 훈련집합을 일정한 크기의 부분집합으로 나눈 후에 부분 집합 별로 처리
8. 다층 퍼셉트론이 학습하는 알고리즘에 대해 설명하시오
오류 역전파 알고리즘 채택 : 출력층에서 시작하여 역방향으로 오류를 전파한다는 뜻에서 오류 역전파라고 부름.
'파이썬으로 만드는 인공지능' 카테고리의 다른 글
| [A.I] 파이썬으로 만드는 인공지능 5장 (0) | 2024.06.07 |
|---|---|
| [A.I] 응용 사례 : 나이브 베이즈 영화 추천 (0) | 2024.06.06 |
| [A.I] 파이썬으로 만드는 인공지능 3장 (0) | 2024.06.03 |
| [A.I] 파이썬으로 만드는 인공지능 2장 (0) | 2024.06.03 |
| [A.I] 파이썬으로 만드는 인공지능 1장 (0) | 2024.06.03 |
