5장 딥러닝과 텐서플로
이 장에서는 직접 구현하는 내용이 많다.
나는 역시나 블로그에는 개념적인 부분만 정리해보고자한다
1980년대 깊은 신경망: 구조적으로는 다층 퍼셉트론에 은닉층을 많이 두면 그것이 깊은 신경망
→ 그레이디언트 소멸문제, 적은 데이터셋, 과다한 계산 시간 등의 이유로 학습이 잘 안됨.
딥러닝의 기술 혁신 요인
- 값 싼 GPU의 등장
- 커진 데이터 셋의 크기
- 학습을 효과적으로 할 수 있는 알고리즘의 등장
텐서란? 딥러닝에서 다차원의 배열을 텐서라고 부름
데이터를 텐서로 표현하고, 신경망의 가중치를 텐서로 표현한다.
텐서의 구조
1차원 : iris 샘플 하나
2차원: iris 샘플 여러개, 명암 영상 한 장
3차원: 명암 영상 여러 장, 컬러 영상 한장
4차원: 컬러 영상 여러 장, 컬러 동영상 여러 장
5차원: 컬러 동 영상 여러개
텐서플로로 퍼셉트론을 프로그래밍 하면 발생하는 문제점
→ 신경망을 직접 코딩해야함 → 이를 해결하기 위해 탄생한 것이 케라스
케라스 클래스의 중요한 3가지 하위 클래스
- models 클래스: Sequential과 functional API 모델 제작 방식 제공(functional은 잘 안씀)
- layers 클래스: 다양한 종류의 층 제공
- optimizes 클래스: 다양한 종류의 옵티마이저 제공
케라스 프로그래밍의 전형적인 절차: 데이터 구축→ 신경망 구조 설계→ 신경망 학습→ 학습된 신경망으로 예측
깊은 다층 퍼셉트론이란 무엇이냐 → 다층 퍼셉트론에서 은닉층을 더 많이 추가하면 깊은 다층 퍼셉트론
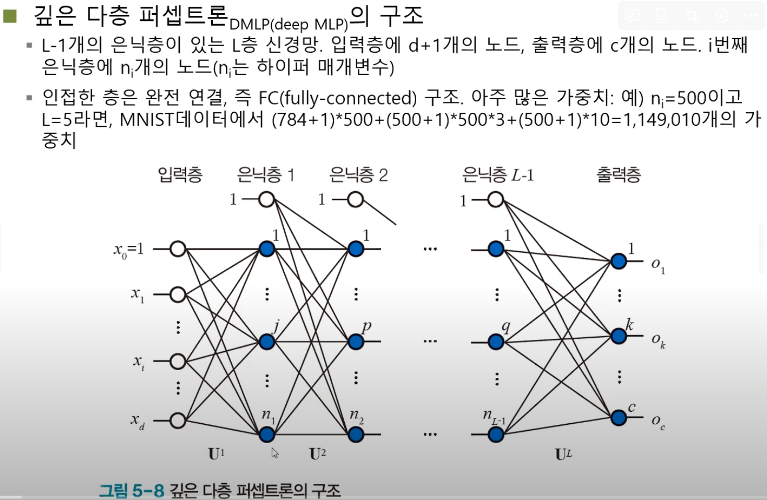
하지만 층이 깊어지면 현실 적인 문제가 발생한다
- 그라디언트 소멸 문제: 은닉층이 많은 깊은 다층 퍼셉트론에서, 은닉층을 많이 거쳐갈 수록 전달되는 오류가 크게 줄어들어 학습이 잘 되지 않는 현상이 발생하는데 이를 그라디언트 소멸(기울기 소멸) 문제라고 한다. 기울기가 0으로 소멸되어 버리면 학습이 매우 느려지고, 학습이 다 이루어지지 않았음에도 멈출 가능성이 존재한다(지역 최솟값에 도달한다고도 칭함).
ex) 시그모이드 함수는 출력 값이 1 아래이므로 소멸 문제가 빠르게 발생함.(0보다 작은 수끼라 곱하면서 연산하면 결과 값이 점점 0으로 수렴하는 현상)’
→해결방안은 사라져가는 성질을 갖지 않는 비선형 함수를 활성화 함수로 선택하면 된다.(ex ReLu함수는 s가 음수일 때 그레디언트는 0, 양수일 때 1) ,혹은 GPU를 사용하거나 TPU 사용
- 과잉 적합 문제: 모델이 훈련 데이터에만 너무 잘 맞게 학습이 되어 정작 테스트 환경에서 새로운 데이터에 새한 예측이나 분류를 제대로 수행하지 못하는 상태(데이터 복잡도에 비해 너무 큰 용량의 모델 사용) . → 일반화 능력 저하
→ 해결방안으로는 데이터 개수 늘리기, 적정한 파라미터 선정, 훈련 데이터를 덜 구체화, 검증된 데이터 셋을 이용하기 등을 채택
2-1: 과소 적합 문제: 모델이 너무 지나치게 단순하여 데이터의 내재된 구조 및 패턴을 학습하지 못하는 경우 발생
→ 해결방안으로는 파라미터가 더 많은 복잡한 모델을 사용하거나, 모델의 하이퍼 파라미터 값을 줄이는 방법 채택
당연한 얘기지만 리프래쉬를 위해서 오차가 크면 갱신이 많아야 하고, 오차가 적으면 갱신도 적어야 한다.
여기서 발생하는 문제 중 평균제곱오차(MSE)는 오차가 크거나 작을때 그레디언트가 비슷한 상황이 발생하거나 반대로 역전 당하는 경우가 발생 → 학습이 느리거나 되지 않는 경우 초래
엔트로피: 무작위성, 불확실성을 의미 → 예를 들어 고체는 엔트로피가 낮다 why? 고체는 항상 일정한 형태를 유지하고 있기 때문 / 기체는 불확실성이 크다 엔트로피도 역시 크다
주사위를 예를 들어, 찌그러진 주사위는 넓어진 면적에 따라 다음에 나올 숫자에 대한 예측 가능성이 높아지기 때문에 엔트로피가 낮아진다. 그래서 기존에 1/6 확률의 공정한 주사위가 예측이 더 어려움으로 엔트로피가 높다라고 할 수 있다 (예측 쉽다고 엔트로피가 높은게 아니고, 예측이 불가능해야 높은 것)
교차 엔트로피란 두 확률 분포 A 와 B의 다른 정도를 측정하는 함수
ex) 공정한 주사위 두개의 교차 엔트로피, 공정한 주사위와 찌그러진 주사위의 교차 엔트로피
교차 엔트로피 손실함수는 평균제곱오차의 불공정성 문제를 해결해준다
'파이썬으로 만드는 인공지능' 카테고리의 다른 글
| [A.I] 파이썬으로 만드는 인공지능 7장 (0) | 2024.06.09 |
|---|---|
| [A.I] 파이썬으로 만드는 인공지능 6장 (0) | 2024.06.08 |
| [A.I] 응용 사례 : 나이브 베이즈 영화 추천 (0) | 2024.06.06 |
| [A.I] 파이썬으로 만드는 인공지능 4장 (0) | 2024.06.05 |
| [A.I] 파이썬으로 만드는 인공지능 3장 (0) | 2024.06.03 |
