
Optimizer
기본적으로 우리는 DB에 데이터를 조회할 때, SQL 쿼리를 보내고 응답을 받는다.
하지만 쿼리에 따라 결과는 동일하지만 내부적으로는 그 결과를 만들어내는 방법은 매우 다양한다. 이렇게 각 테이블의 데이터가 어떤 분포로 저장되어 있는지를 통계 정보를 참조하여 기본 데이터를 비교해 최적의 실행계획을 수립하는 작업을 해주는 것이 옵티마이저이다.
Storage Engine
스토리지 엔진은 데이터의 저장소로써, 옵티마이저가 제공한 실행계획에 따라 스토리지 엔진이 실제 데이터를 읽어온다.
여러 스토리지 엔진이 존재하지만, MySQL에서는 우리가 가장 흔하게 들어본 InnoDB가 사용된다.
옵티마이저와 스토리지 엔진이 최적의 방식으로 데이터를 가져오는 과정

우리가 DB에 쿼리를 날리게 되면, 옵티마이저는 어떻게 최적의 실행계획을 세울지 고민을 하기 시작한다.
스토리지 엔진에 저장딘 데이터가 다양하기 때문에, 동일한 데이터라도 다양한 인덱스가 존재할 수 있기 때문이다.
옵티마이저 입장에서는 어떤 방식이 효율적인지 판단하기 위해선 데이터를 기반으로 판단해야한다.
우리가 가져오려는 데이터의 양, 특성에 따라 어떤 방식이 가장 효율적인지 판단하기 위해 정량적 지표인 통계 데이터라는 것을 보게 된다(사실 DB는 우리 몰래 백그라운드서 효율적인 탐색을 위해 데이터를 통계내고 있다.)
예를 들면 인덱스의 크기, 테이블의 크기, 컬럼 통계등을 저장하고 있다.

이러한 통계 수치를 보고 옵티마이저는 어떤 방식이 가장 효율적인지 판단하게 되는데, 그 판단의 방식을 바로 쿼리 플랜 이라고 한다.
Query Plan
쿼리 플랜은 DBMS가 SQL 을 처리하기 위해 사용하는 실행 계획인데, 이를 통해 데이터를 검색하고 가져오는 방법을 결정하는데 사용한다.
즉, 옵티마이저가 SQL을 실행하는데 있어 사용되는 비용과 어떤 방식이 효율적인지 판단하고 올바른 플랜중에서 가장 적절한 순서와 방식으로 처리 되는 방식을 스토리지 엔진에 전달하게 되고, 그 시점에 스토리지 엔진이 해당 데이터를 찾아오게 된다.
Query Plan 선택
웬만하면 석박사님들이 만들어주신 옵티마이저는 최적의 알고리즘으로 매우 효율적인 선택지를 결정한다.
다만 가끔 맘에 들지 않는 경로로 탐색을 시도하는데, 이것이 바로 인덱스가 필요한 시점이다. 즉, 우리가 적절한 인덱스를 추가해주지 않아서 구린 선택지를 가는 경우가 있다.
그래서 우리 개발자가 할 작업은 옵티마이저가 적절한 길을 찾을 수 있도록 도로를 포장해주는 인덱싱 작업이 필요하다.
MySQL Workbench가 이 상황에 가장 최적의 도구로 사용되어지는데, 쿼리 플랜을 가시적으로 보여준다.
우리는 이런 쿼리 플랜을 보고 옵티마이저의 생각을 읽고, 적절한 방식을 택하지 못하고 있다면 적절한 방식을 택하도록 인덱스를 설정해주어야 한다.
쿼리 플랜 보는 명령어
desc select * from book;쿼리 앞에 desc만 붙여주면 된다.

다음과 같은 내용들이 있는데, 우리가 주요하게 봐야할 항목들은 다음과 같다.
1. type : 테이블에 있는 데이터를 어떤 방식으로 조회 했는지에 대한 정보
2. possible_keys : 사용할 수 있는 인덱스 목록
3. key : 데이터 조회시 실제 사용한 인덱스
4. rows : sql실행시 테이블에 접근한 개수 -> 이 엑세스 수가 많을수록 시간소요가 커짐 -> 이 값을 줄이는게 쿼리 튜닝의 핵심
5. filtered : Where 문와 같은 필터 조건에 따라 어느정도 데이터가 남아 있는지에 대한 정보
(참고로 rows와 filtered는 추정치)
type
쿼리플랜에서 우리가 가장 첫번째로 확인해야할 것은 타입이다.
ALL 타입
ALL 타입은 모든 테이블을 다 본다는 의미이다.
옵티마이저 입장에서 이 데이터를 다 가져오기 위해서 가장 수월한 방식이 뭐냐고 고민했을 때, 결국 모든 테이블을 다 봐야한다는 의미이다.
ALL 은 공포의 Full Table Scan을 의미하고, 인덱스를 사용하지 않으며 테이블으 처음부터 끝까지 다 뒤지는 완전 탐색을 의미한다.
주로 인덱스가 없을 때 발생하고, B+트리 사용 X, 그리고 전체 테이블을 스캔하며 당연히 가장 비효율적인 방식이다.
좀더 자세히 해당 쿼리에 대한 플랜을 분석하고 싶다면 다음 쿼리를 입력해보자.
DESC ANALYZE SELECT * FROM book;간단히 말하자면 ANALYZE 키워드를 통해 데이터베이스가 어떻게 쿼리를 처리하고, 어떤 연산을 통해 결과를 얻었는지, 그리고 예상 비용, 실제 처리할 행, 소요 시간등을 알려준다.
그럼 대충 아래와 같은 결과를 얻는데,
Table scan on book (cost=100520 rows=996789) (actual time=0.248..190 rows=1e+6 loops=1)결과를 해석해보면
1. Table scan on book -> 쿼리를 수행할 때 book 테이블 전체에 대해 스캔
2. cost = ... rows = ..... -> 옵티마이저가 추정한 값으로써 cost는 연산처리비용을 나타내고, row는 예상 도는 반환 행 수를 나타낸다.
당연히 연산 처리 비용이 낮을 수록 좋다.
3. acutal time = .... row = .... loops = .... -> 실제 실행시 예측되는 시간이다.
actual time = 쿼리 시작부터 종료까지의 최소 ~ 최대 처리 시간을 밈미초 단위로 나타낸 것
row = 실제 처리 된 레코드 수를 의미한다.
loops = 이 연산이 한번만 반복되었음을 의미한다.
정리하면, 데이터베이스가 book 테이블을 통째로 스캔하여 대략 100만건 정도의 데이터를 처리했고, 그 과정을 보여준다 라고 생각하면 된다.
참고로 워크 벤치는 이런 쿼리 플랜을 그래프로 보여주는데, 풀 테이블 스캔시 아래처럼 나타내준다.

range type
이제 인덱스 생성 후 범위 검색을 해보자.
CREATE INDEX idx_price ON book(price);book 테이블에 가격에 대해 인덱스를 생성했다.
예를 들어 10000원 ~ 20000원 사이 책을 찾는다고 해보자. (대충 쿼리는 WHERE price BETWEEN 10000 AND 20000)
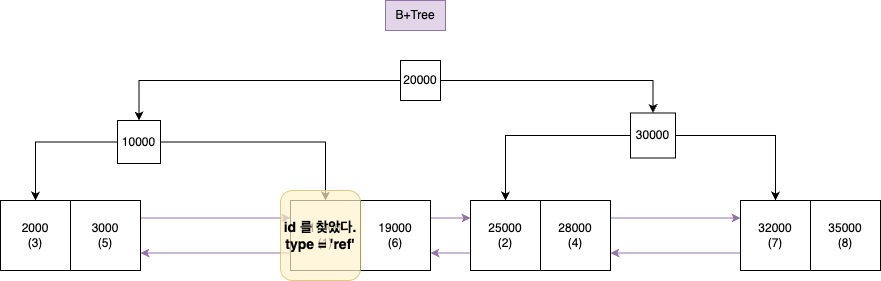
B+트리 기준으로 루트 노드에서 10000이 있는 리프 노드까지 내려가서 20000 리프 노드까지 순차적으로 스캔을 한다.

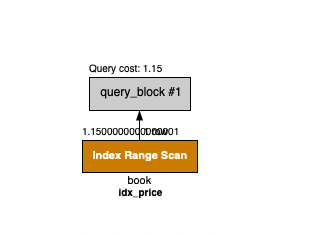
특정 범위의 노드만 읽으면 되므로 ALL 보다는 효율적인 방식이다.
ref type
이번엔 인덱스가 존재하는 상태에서 동등조건을 따져보자.
SELECT * FROM book WHERE price = '11000';위에서 price에 대한 인덱스가 이미 존재하기 때문에, 동등 연산시 type이 ref로 반환된다.
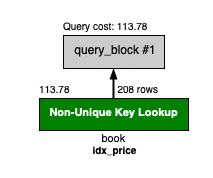
B+트리 관점에서 루트 노드부터 11000이 위치한 리프 노드까지 한번에 찾아갈 수 있게 되어 range보다 더 효율적인 탐색이 가능해진다.
const type
const type은 PK인덱스나 UNIQUE 인덱스 사용시 나타난다.
SELECT * FROM book WHERE id = 1;

루트노드부터 리프노드까지 정확히 하나의 리프노드를 찾아갈 수 있게 되었다.
이때, PK는 UNIQUE하므로 더이상 탐색이 필요가 없다.
유일한 하나의 값만 찾기 때문에 유니크 인덱스로 하나의 행을 찾을 때 가장 효율적인 검색 타입이다.
index type
인덱스 타입은 말 그대로, 이미 인덱스가 있는데 인덱스에 존재하는 칼럼을 조회하도록 쿼리를 실행하면 발생한다.
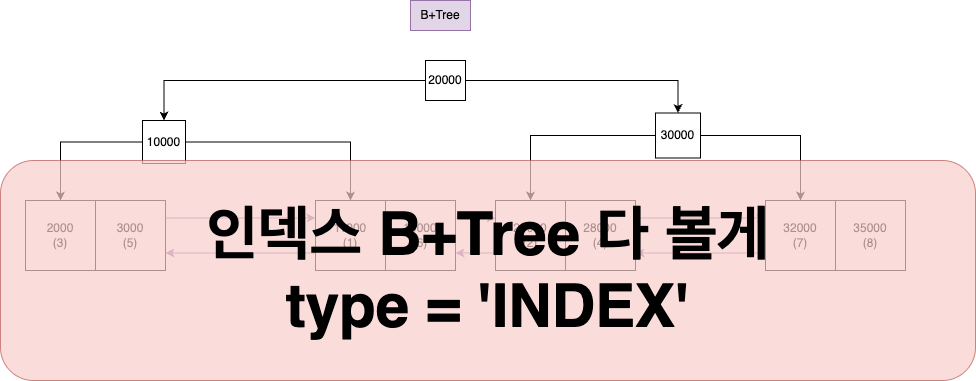

하지만 이는 실제 테이블의 데이터를 인덱스가 가지고 있어 실제 테이블을 조회할 필요가 없기 때문에 효율적일 수도 있다.(커버링 인덱스)
이 상황에서는 결국 인덱스 전체 (B+트리 전체)를 뒤져야 하기 때문에 ALL 보다는 낫지만, 그다지 효율적인 방식은 아니다.
결론
대충 const > ref > range > index > ALL 정도로 성능이 좋은데, 옵티마이저에 따라 쿼리 플랜은 유동적으로 변경된다. (특히 데이터 적을 때는 FULL SCAN이 빠를 수도 있음)
쿼리 플랜의 절대적인 것은 없으니 성능 수식은 참고 정도만 하고 유동적으로 실제 성능에 영향이 큰 부분부터 점검하고 개선하는 것이 올바른 쿼리 튜닝 방법이다.
'우리 같이 백엔드 하자 > Index' 카테고리의 다른 글
| Index 3편 - (논) 클러스티드 인덱스, 커버링 인덱스 (0) | 2025.12.17 |
|---|---|
| Index 2편 - Index 구현 (B+Tree) (1) | 2025.12.15 |
| Index 1편 - 단일인덱스와 복합인덱스 (0) | 2025.12.15 |
