이진 트리 / 완전 이진 트리
이진트리란 노드에 최대 2개의 자식 노드만 올 수 있는 트리 자료구조이다.
이때, 해당 레벨의 왼쪽부터 차례차례 원소가 쌓이게 되면 완전 이진트리라고 한다.
예를 들면 좌측은 완전 이진 트리이고, 오른쪽은 완전 이진트리가 아니다.
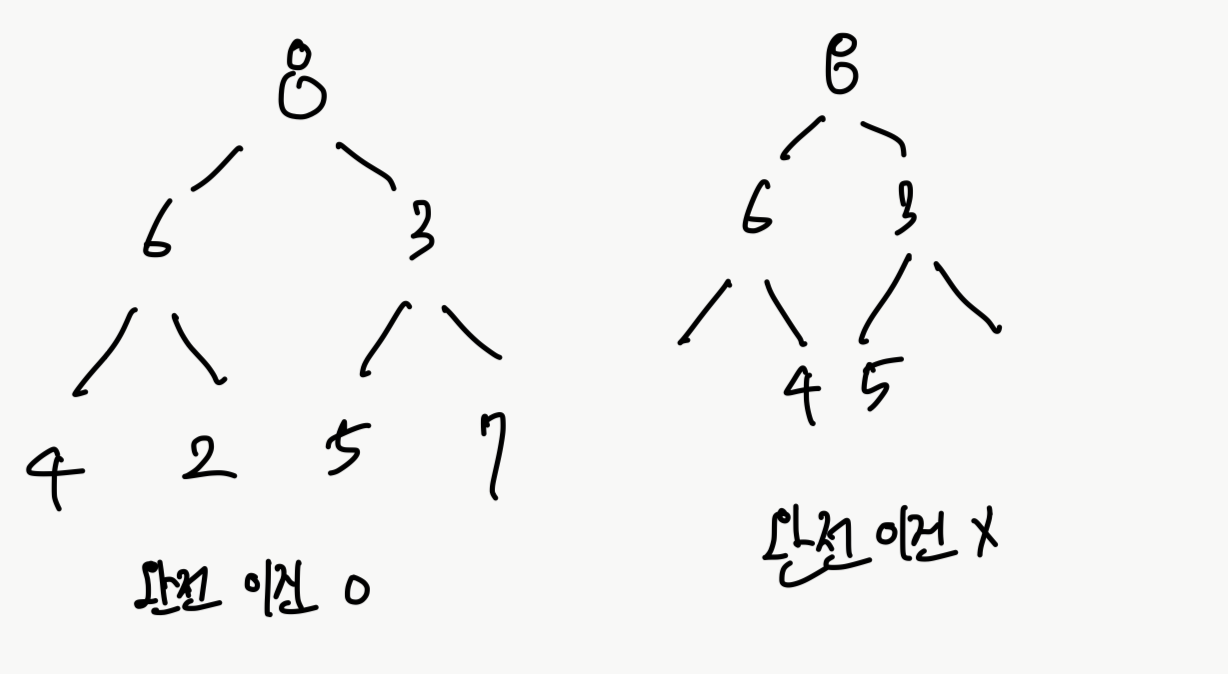
이런 트리는 배열로 표현할 수 있는데, 위 예시대로 표현 하자면 다음과 같다.
-> [null, 8, 6, 3, 4, 2, 5, 7]
이때 0번째 인덱스는 편의상 비워두고 1번째 인덱스부터 사용한다.
이제 그려면 규칙성이 하나 보이는데, 현재 인덱스를 기준으로 자식 인덱스를 찾을 수 있는 공식이 보이고, 자식 인덱스 기준 본인의 부모 인덱스를 찾을 수 있는 공식도 보인다.
자식 <-> 부모노드 구하는 공식
* 부모의 왼쪽 자식 노드 구하기 : 현재 Index * 2
* 부모의 오른쪽 자식 노드 구하기 : 현재 Index * 2 + 1
* 자식의 부모 노드 구하기 : 현재 Index / 2 (나머지 버림)이런식으로 구현 해두면, 쉽게 부모와 자식 인덱스를 비교할 수 있게 된다.
완전 이진트리의 시간복잡도
또한, 만약 높이가 h 라면 노드의 개수도 쉽게 구할 수 있는데, 공식은 다음과 같다 -> 2(h + 1)−1
이때 최대 노드의 개수가 N 개라고 하면 N = 2(h + 1) - 1 이란 수식을 세울 수 있고, 이를 다시 h에 대해 정리하면
h = log_2 (N + 1) - 1 로 표현할 수 있다.
이때 완전 이진트리의 노드 개수가 N일 때, 높이가 log_2 (N + 1) - 1 이므로, 아무리 높아봤자 O(log(N)) 의 시간복잡도가 나온다.
힙 (Heap)
힙 자료구조는 데이터의 최대 || 최소를 빠르게 찾기 위해 구현된 완전 이진트리 형태의 자료구조이다.
힙의 특성은 항상 큰값 (혹은 작은값)이 상위 레벨에 있고, 작은 값(혹은 큰값)이 하위 레벨에 있어야하는 규칙을 가진 자료구조이다.
즉 부모의 값이 자식 노드보다 반드시 커야(작아야)한다.
그러면 가장 큰 값(혹은 작은값)은 루트노드쪽으로 가게 되고, 우리는 O(1)로 한번에 최대 || 최소 값을 찾을 수 있게 된다.
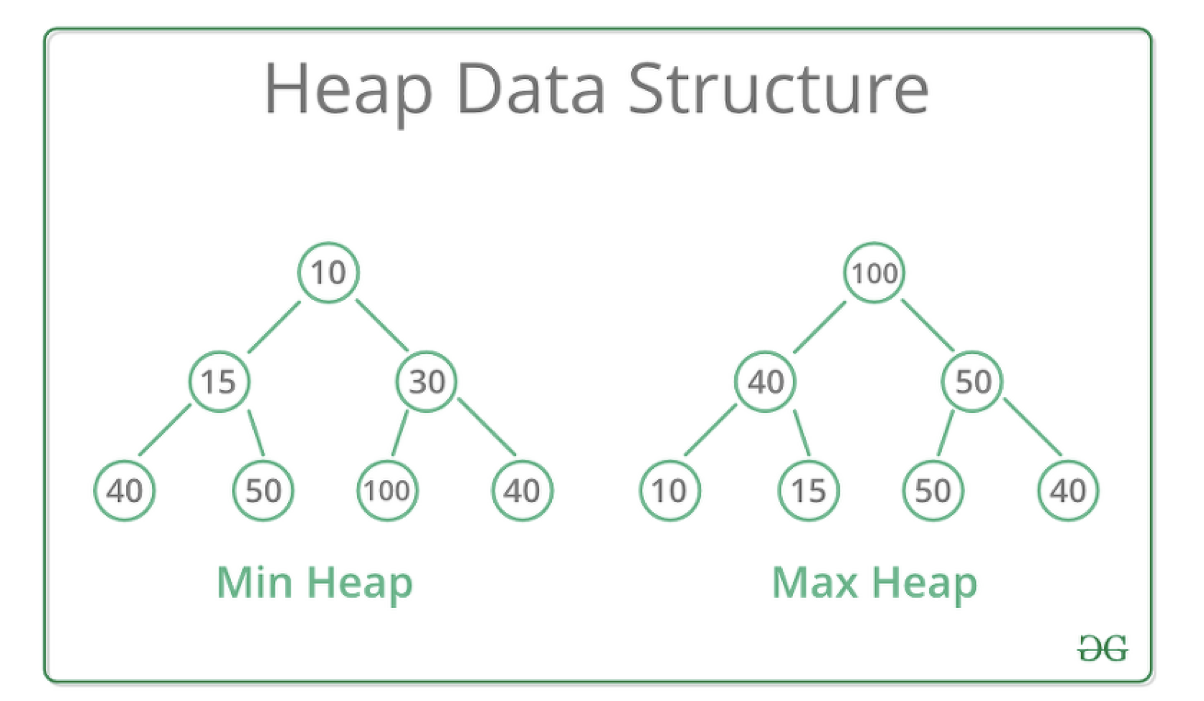
이제 이러한 힙의 특성에 따라 원소를 추가하고 삭제하는 과정을 보자 (주석 참조).
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
List<Integer> items;
public MaxHeap() {
this.items = new ArrayList<>();
this.items.add(null); // 이진트리를 쉽게 쓰기 위해 0번째 인덱스 사용 X -> null 삽입
}
public void insert(int value) {
// 먼저 원소를 제일 뒤에 추가
items.add(value);
// 본인의 현재 인덱스 기록
int currentIndex = this.items.size() - 1;
// 추가한 값이 자신의 부모노드보다 클 때 부모노드와 자신의 위치를 swap
while (currentIndex != 1) { // 첫번째 탈출 조건은 삽입한 노드가 루트 노드가 되면 종료
int parentIndex = currentIndex / 2;
/**
* 자식 <-> 부모노드 구하는 공식
* 부모의 왼쪽 자식 노드 구하기 : 현재 Index * 2
* 부모의 오른쪽 자식 노드 구하기 : 현재 Index * 2 + 1
* 자식의 부모 노드 구하기 : 현재 Index / 2 (나머지 버림)
*/
// 부모 노드와 비교 -> 부모보다 크다면 swap
if (this.items.get(currentIndex) > this.items.get(parentIndex)) {
int temp = this.items.get(currentIndex);
this.items.set(currentIndex, this.items.get(parentIndex));
this.items.set(parentIndex, temp);
currentIndex = parentIndex; // swap 하게 되면 현재 추가한 원소가 부모 노드가 된다
} else { // 만약 위 조건이 아니라면? -> 이미 부모 노드가 자식 노드보다 큰 상태
break;
}
}
}
// max value 제거
// 기존 루트노드 삭제 -> 이후 아래로 내려가면서 부모와 자식 노드 비교
// 원소 제거 로직의 탈출 조건은 부모 노드 값이 자식노드 두개보다 반드시 커야함 && size-1 도달시 탈출
public int delete() {
// 1. 먼저 마지막 노드와 루트노드 교체
int temp = this.items.get(1);
this.items.set(1, this.items.get(this.items.size() - 1));
this.items.set(this.items.size() - 1, temp);
// 여기까지 오면 현재 노드 순서 바뀜
// 2. 마지막 노드(루트 노드였던 것) 삭제 (나중에 반환해야 함)
int prevMax = this.items.remove(this.items.size() - 1);
int currentIndex = 1; // 비교 시작 지점 (루트 노드)
while (currentIndex <= this.items.size() - 1) {
/**
* 자식 <-> 부모노드 구하는 공식
* 부모의 왼쪽 자식 노드 구하기 : 현재 Index * 2
* 부모의 오른쪽 자식 노드 구하기 : 현재 Index * 2 + 1
* 자식의 부모 노드 구하기 : 현재 Index / 2 (나머지 버림)
*/
int leftChildIndex = this.items.get(currentIndex) * 2;
int rightChildIndex = this.items.get(currentIndex) * 2 + 1;
int maxIndex = currentIndex; // 지금 부모 노드가 가장 크다고 가정
// 만약 좌측 자식 노드의 인덱스가 마지막이 아니고 , 좌측 자식 노드의 현재 값이 부모보다 크다면?
if (leftChildIndex <= this.items.size() - 1
&& this.items.get(leftChildIndex) > this.items.get(maxIndex)) {
maxIndex = leftChildIndex; // 좌측 자식 노드가 크다고 업데이트
}
// 만약 우측 자식 노드의 인덱스가 마지막이 아니고 , 좌측 자식 노드의 현재 값이 부모보다 크다면?
if (rightChildIndex <= this.items.size() - 1
&& this.items.get(rightChildIndex) > this.items.get(maxIndex)) {
maxIndex = rightChildIndex;
}
if (maxIndex == currentIndex) {
break;
}
// 여기 조건문까지 끝나면 부모 - 좌측 자식 - 우측 자식 노드중 가장 큰 값이 나옴
// 현재 부모 노드와 maxIndex의 값을 swap
int leftChildIndex = currentIndex * 2;
int rightChildIndex = currentIndex * 2 + 1;
int maxIndex = currentIndex; // 지금 부모 노드가 가장 크다고 가정
// 여기서 끝나면 안되고, 현재 인덱스에 최근까지 수정한 자식 노드의 인덱스를 넣어줘야 추가로 탐색 가능
currentIndex = maxIndex;
}
return prevMax;
}
public static void main(String[] args) {
MaxHeap maxHeap = new MaxHeap();
maxHeap.insert(3);
maxHeap.insert(4);
maxHeap.insert(2);
maxHeap.insert(9);
System.out.println(maxHeap.items); // [null, 9, 4, 2, 3] 가 출력되어야 함
}
}
'Algorithm' 카테고리의 다른 글
| [Algorithm] 알파벳 찾기 - 백준 10809 (0) | 2025.06.12 |
|---|---|
| [Algorithm] 최빈값 찾기 (0) | 2025.06.11 |
| [Algorithm] 봉우리 (0) | 2025.05.23 |
| [Algorithm] 격자판 최대 합 (0) | 2025.05.23 |
| [Algorithm] 보이는 학생 -> 입력 및 복잡도 생각하고 풀기 (0) | 2025.05.08 |
